Find the midpoint of rs – Finding the midpoint of RS is a fundamental concept in geometry that involves determining the exact middle point of a line segment. This guide will delve into the concept of midpoints, explore their applications, and provide practical methods for finding them.
From understanding the formula to constructing midpoints using geometric tools, this guide covers everything you need to know about finding midpoints in various scenarios.
Understanding Midpoints
Midpoints play a crucial role in geometry and other mathematical applications. They help us locate the exact center or balance point of a line segment. Understanding the concept of midpoints is essential for solving various problems and understanding geometric relationships.
The midpoint of a line segment is the point that divides the segment into two equal parts. It is denoted by the letter M. To find the midpoint of a line segment with endpoints (x1, y1) and (x2, y2), we use the midpoint formula:
M = ((x1 + x2) / 2, (y1 + y2) / 2)
To find the midpoint of RS, we can use the midpoint formula. In other news, a gas occupies 900.0 ml , which is quite a bit of volume. Returning to our original problem, once we have the coordinates of the midpoint, we can plot it on a graph.
Application of Midpoint Formula
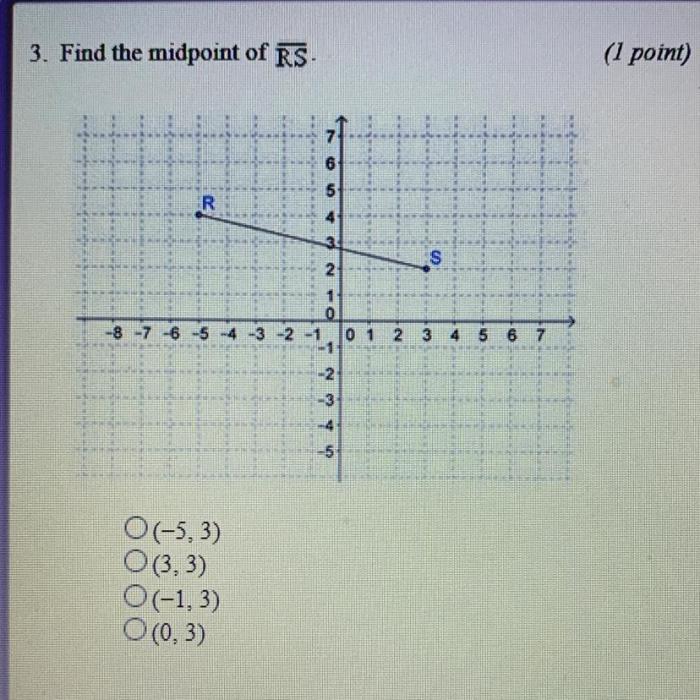
The midpoint formula is a mathematical tool that allows us to find the exact middle point of a line segment. It is widely used in geometry, engineering, and other fields that involve spatial calculations.
The formula for finding the midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is:
$$M = (\fracx1 + x22, \fracy1 + y22)$$
Using the Midpoint Formula
To use the midpoint formula, simply plug in the coordinates of the two endpoints into the formula. For example, to find the midpoint of a line segment with endpoints (2, 3) and (6, 9), we would do the following:
$$M = (\frac2 + 62, \frac3 + 92)$$$$M = (4, 6)$$
Therefore, the midpoint of the line segment with endpoints (2, 3) and (6, 9) is (4, 6).
Applications of the Midpoint Formula, Find the midpoint of rs
The midpoint formula has a wide range of applications in various fields, including:
- Geometry:Finding the center of a circle, midpoint of a line segment, and the centroid of a triangle.
- Engineering:Calculating the center of gravity of an object, determining the midpoint of a bridge, and designing symmetrical structures.
- Computer Graphics:Finding the center of a pixel, calculating the midpoint of a line segment for interpolation, and creating symmetrical images.
- Physics:Determining the center of mass of an object, calculating the midpoint of a trajectory, and analyzing the motion of objects.
Midpoints in Coordinate Geometry: Find The Midpoint Of Rs
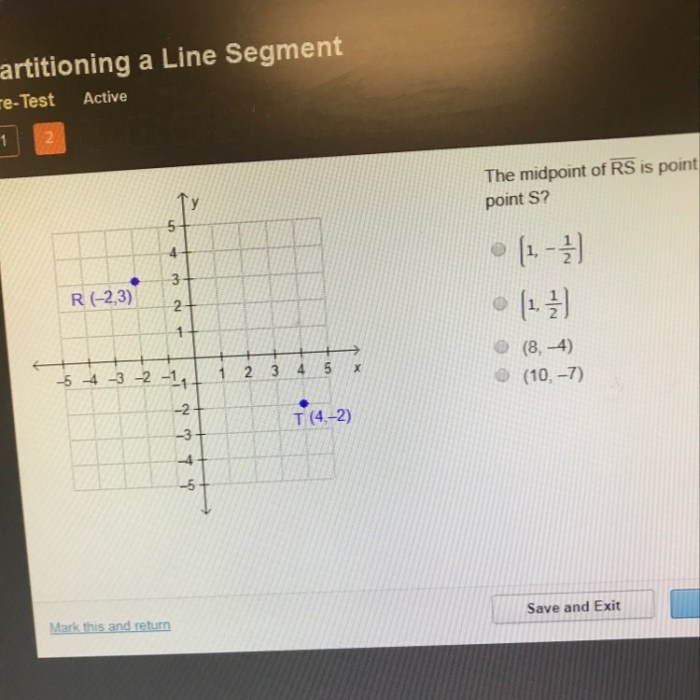
Midpoints play a significant role in coordinate geometry, providing a way to determine the center point of a line segment or the intersection of two lines. Understanding the relationship between midpoints and coordinates allows us to solve various geometry problems efficiently.
Finding the Midpoint of a Line Segment
Given the coordinates of the endpoints of a line segment, (x1, y1) and (x2, y2), the midpoint (x, y) can be calculated using the midpoint formula:
x = (x1 + x2) / 2y = (y1 + y2) / 2
This formula essentially averages the x-coordinates and y-coordinates of the endpoints to find the midpoint.
Geometric Constructions
Geometric constructions involve using tools like a compass and straightedge to create geometric shapes and figures. These constructions can be used to find the midpoint of a line segment.
Method 1: Perpendicular Bisector
This method involves constructing a perpendicular bisector of the line segment, which is a line that intersects the segment at its midpoint and is perpendicular to it.
- Draw the line segment RS.
- Place the compass point on one endpoint, R, and draw an arc that intersects the segment.
- Repeat step 2 with the compass point on the other endpoint, S.
- The two arcs will intersect at two points, A and B.
- Draw a line through points A and B. This line will be the perpendicular bisector of RS.
- The midpoint of RS is the point where the perpendicular bisector intersects RS.
Method 2: Midpoint Compass Method
This method uses a compass to directly find the midpoint of a line segment.
- Draw the line segment RS.
- Open the compass to a width greater than half the length of RS.
- Place the compass point on one endpoint, R, and draw an arc that intersects the segment.
- Without changing the compass width, place the compass point on the other endpoint, S, and draw another arc that intersects the segment.
- The two arcs will intersect at two points. The midpoint of RS is the point where these arcs intersect.
Method 3: Paper Folding Method
This method uses paper folding to find the midpoint of a line segment.
- Draw the line segment RS on a piece of paper.
- Fold the paper along the line segment RS.
- Unfold the paper and the crease will be the perpendicular bisector of RS.
- The midpoint of RS is the point where the crease intersects RS.
Applications in Real-Life Scenarios
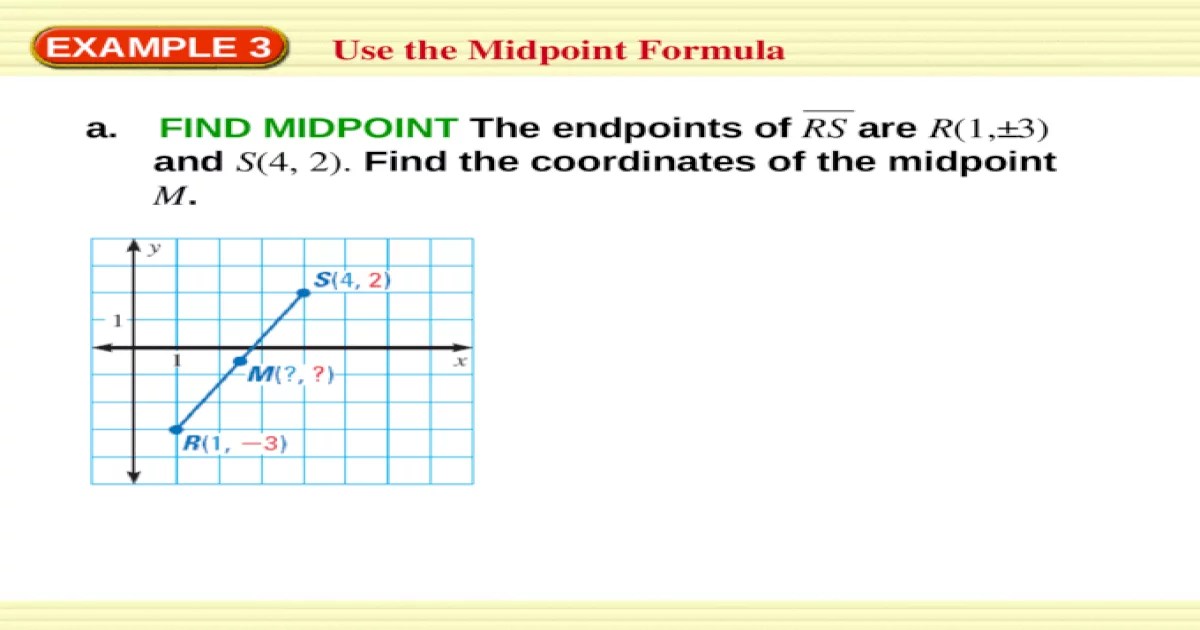
Finding midpoints has numerous practical applications in various fields. From architecture and engineering to everyday life, the concept of midpoints plays a crucial role in ensuring accuracy, balance, and efficiency.
Architecture
In architecture, finding the midpoint is essential for determining the center of a room, wall, or other architectural feature. This helps ensure symmetry and balance in the design, creating visually appealing and harmonious spaces.
For example, when designing a rectangular room, finding the midpoint of the opposite walls allows architects to position windows, doors, and other elements symmetrically, creating a sense of equilibrium and order.
Engineering
In engineering, finding midpoints is critical for structural stability and load distribution. Engineers use midpoints to calculate the center of gravity of objects, which is essential for ensuring that structures can withstand forces without collapsing.
For instance, in designing a bridge, engineers need to find the midpoint of the span to determine where the main support should be placed. This ensures that the bridge can carry its intended load safely and efficiently.
Everyday Life
Finding midpoints also has practical applications in everyday life. For example, when folding a piece of paper in half, finding the midpoint helps ensure that the fold is even and symmetrical.
Additionally, when hanging a picture on a wall, finding the midpoint of the picture and the wall helps align it properly, ensuring that it is centered and visually appealing.
Extensions and Variations
The midpoint formula is a versatile tool that can be extended and varied to suit different types of curves and applications.
Variations of the Midpoint Formula for Different Types of Curves
The standard midpoint formula works for straight lines. However, there are variations of the formula that can be used to find the midpoints of other types of curves, such as parabolas, circles, and ellipses.For example, the midpoint of a parabola with equation $y = ax^2 + bx + c$ is given by the formula:$$\left(\frac-b2a, \fracb^2
4ac4a\right)$$
Similarly, the midpoint of a circle with equation $(xh)^2 + (y
k)^2 = r^2$ is given by the formula
$$\left(h, k\right)$$
Applications of Midpoints in Other Areas of Mathematics
Midpoints also have applications in other areas of mathematics, such as calculus and statistics.In calculus, midpoints are used to find the average value of a function over an interval. In statistics, midpoints are used to find the median of a dataset.
Query Resolution
What is the midpoint of a line segment?
The midpoint is the point that divides a line segment into two equal parts.
How do I find the midpoint of a line segment using coordinates?
Use the midpoint formula: ((x1 + x2) / 2, (y1 + y2) / 2), where (x1, y1) and (x2, y2) are the coordinates of the endpoints.
What are some practical applications of finding midpoints?
Midpoints are used in architecture, engineering, and everyday life to locate the center of objects, divide spaces evenly, and solve geometric problems.