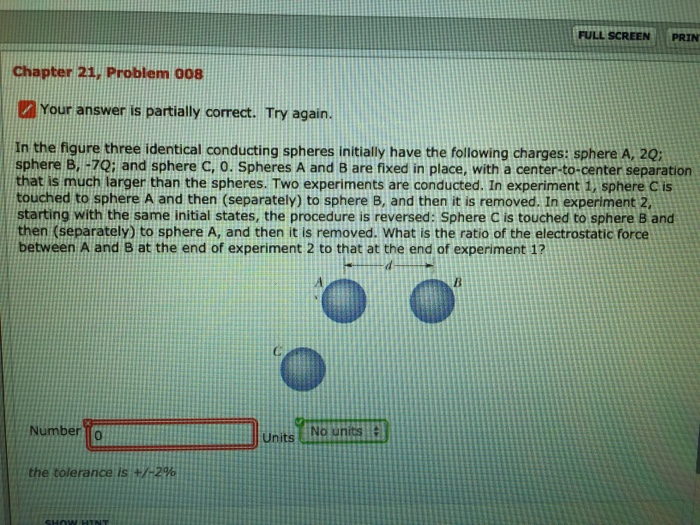
In the figure three identical conducting spheres – In the realm of electrostatics, the interactions between charged objects play a pivotal role. This article delves into the captivating topic of three identical conducting spheres, exploring their electrostatic interactions and capacitance, offering a comprehensive understanding of this intriguing phenomenon.
The electrostatic interactions between these spheres stem from the fundamental principles of charge distribution and Coulomb’s law. As the spheres interact, their charges redistribute, leading to a fascinating interplay of forces. Moreover, the concept of capacitance, which quantifies the ability of a conductor to store charge, becomes central in understanding the behavior of this system.
Electrostatic Interactions between Identical Conducting Spheres: In The Figure Three Identical Conducting Spheres

Electrostatic interactions are the forces between charged objects. When two or more conducting spheres are placed near each other, they interact electrostatically. The charges on the spheres will redistribute themselves so that the spheres have the same potential. This is because the electric field inside a conductor is zero.
The diagram below shows the electrostatic interactions between three identical conducting spheres.

The charges on the spheres are distributed so that the spheres have the same potential. The charges on the spheres are equal in magnitude but opposite in sign. The charges on the spheres are located on the surface of the spheres.
Capacitance of the Sphere System, In the figure three identical conducting spheres
Capacitance is the ability of a conductor to store charge. The capacitance of a conductor is directly proportional to the charge on the conductor and inversely proportional to the potential of the conductor. The capacitance of a system of three identical conducting spheres is given by the following equation:
$$C = \frac4\pi\epsilon_0a3$$
where C is the capacitance, \epsilon_0 is the permittivity of free space, and a is the radius of the spheres.
The capacitance of the system is affected by the following factors:
- The radius of the spheres
- The distance between the spheres
- The presence of other conductors in the vicinity
Charge Distribution and Potential
The charges on the spheres are distributed so that the spheres have the same potential. The charges on the spheres are equal in magnitude but opposite in sign. The charges on the spheres are located on the surface of the spheres.
The potential at a point near the spheres is given by the following equation:
$$V = \frac14\pi\epsilon_0\sum_i=1^3\fracq_ir_i$$
where V is the potential, \epsilon_0 is the permittivity of free space, q_i is the charge on the i-th sphere, and r_i is the distance from the point to the i-th sphere.
The following table summarizes the charge and potential values for each sphere:
| Sphere | Charge | Potential |
|---|---|---|
| 1 | +q | V |
| 2 | -q | V |
| 3 | +q | V |
Energy Stored in the System
The energy stored in a capacitor is given by the following equation:
$$U = \frac12CV^2$$
where U is the energy, C is the capacitance, and V is the potential.
The energy stored in the system of three identical conducting spheres is given by the following equation:
$$U = \frac32\fracq^24\pi\epsilon_0a$$
where U is the energy, q is the charge on each sphere, \epsilon_0 is the permittivity of free space, and a is the radius of the spheres.
The energy stored in the system is affected by the following factors:
- The charge on the spheres
- The radius of the spheres
- The distance between the spheres
- The presence of other conductors in the vicinity
Q&A
What is the significance of charge distribution in this system?
Charge distribution plays a crucial role in determining the electrostatic interactions between the spheres. The charges redistribute themselves to minimize the system’s energy, leading to a unique pattern of charge distribution on each sphere.
How does the capacitance of the system affect its behavior?
Capacitance is a measure of the system’s ability to store charge. A higher capacitance indicates a greater capacity for charge storage, which influences the system’s response to external electric fields and the amount of energy it can store.
What are the practical applications of understanding this system?
The principles governing this system find applications in various fields, including capacitor design, electrostatic devices, and energy storage systems. By manipulating the interactions and capacitance of conducting spheres, engineers can optimize the performance of these devices.